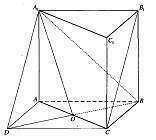
Призма АВСА1В1С1, через ее вершину А1 проведем прямую, которая параллельна диагонали В1С. Точка D пересечение В1С с плоскостью основания призмы АВС.
А1В1 параллельна плоскости АВС и плоскости A1В1СD, значит А1В1 параллельна СD,
а А1В1СD-параллелограмм.
АВ параллельна А1В1 и АВ=А1В1, значит АВ параллельна СD, AB=CD и АВСD-ромб.
диагонали ромба АС и ВD пересекаются под прямым углом в точке О и делятся пополам, значит А1О в равнобедренном треугольнике А1ВD является биссектрисой, медианой и высотой: <ВА1О=<DA1O=1/2<BA1D. <br>Угол между непересекающимися диагоналями А1В и В1С равен углу ВА1D.
Исходя из условия АВ=ВВ1 обозначим через а,
тогда диагональ квадрата А1В=а√2
высота равностороннего треугольника ВО=а√3/2
sin BA1O =BO/A1B=a√3/2a√2=√3/2√2
cos