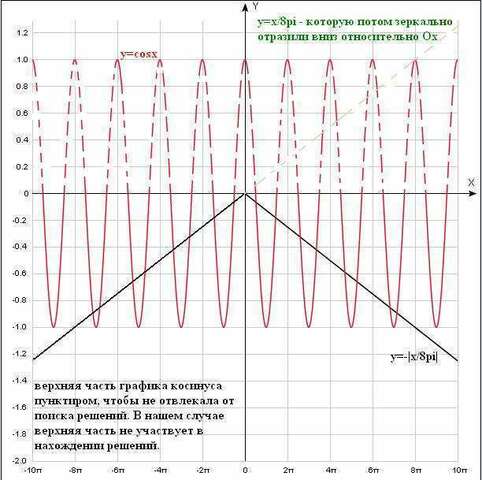
Удобнее всего решать графически, т.к. функции стандартные, графики легко нарисовать, особая точность в рисовании графиков не нужна (т.к. требуется найти количество решений, а не их значения).
Пусть функция слева: 
, функция справа: 
.
Вначале порассуждаем над графиками и свойствами функций.
1) Косинус - периодическая четная функция, период равен 2π.
2) y2 - это прямая, но за счет модуля "ломаная". Для того, чтобы построить эту функцию, необходимо вначале построить график функции 
, а затем ту часть, что расположена выше оси Ох, зеркально отобразить вниз (относительно Ох). Получится перевернутая "галочка" с вершиной в точке (0;0).
3) Теперь найдем интервал, на котором будут пересечения двух графиков. Известно, что 
, значит такие же значения должна принимать и другая функция, т.е.: 
4) 8π для косинуса - это четыре периода. Значит, вправо от оси Оу будет 4 промежутка возрастания и 4 промежутка убывания. Аналогично влево от оси Оу. Итого: 16 промежутков ("кусочков" функции). Соответственно, прямая пересечет график косинуса в 16 точках.
Убедимся в полученном ответе, начертив графики функций: косинус - стандартная функция, ее общий вид необходимо знать; функция по модулю - уже расписано, как начертить. Оба графика чертим в одной координатной плоскости!
Ответ: 16 решений
