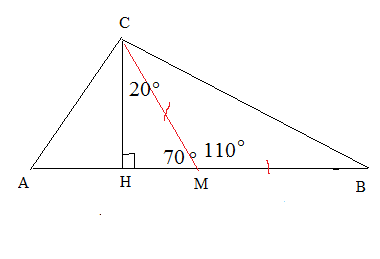Дано: Δ АВС,
∠
С=90° СH ⊥ AB, AM=MB
∠HCM=20°
Δ CHM - прямоугольный (СН ⊥ AB),∠HCM=20°
Сумма острых углов прямоугольного треугольника равна 90° ,
значит ∠HMС=90°-20°=70°
∠CMВ- смежный с углом HMC. Cумма смежных углов равна 180°
∠CMВ=180 °-70°=110°
Треугольник СМВ равнобедренный СМ=МВ.
Медиана прямоугольного треугольника, проведенная из вершины прямого угла равна половине гипотенузы.
∠МВС= ∠ВCM=(180°-110°)/2=35°
Значит острый угол АВС прямоугольного треугольника АВС равен 35°
Сумма острых углов прямоугольного треугольника равна 90°. Второй острый угол
САВ равен 90°-35°=55°
Ответ. 55°- больший острый угол прямоугольного треугольника