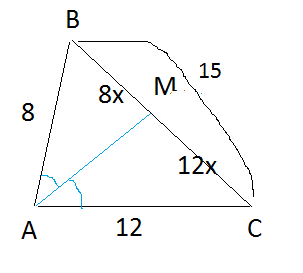
Биссектриса острого угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
AM - биссектриса,
Обозначим
ВМ= 8х
МС= 12х,
тогда отношение 8х:12х=8:12 равно отношению сторон.
Но 8х+12х=15
20х=15
х=15:20
х=3/4
ВМ=8х=8·(3/4)=6
МС=12х=12·(3/4)=9
По теореме косинусов из треугольника
АВС
АС²=АВ²+ВС²-2·АВ·ВС·сos(
∠ B)
12²=8²+15²-2·8·15·сos(
∠ B)
144=64+225- 240·cos(
∠ B)
cos(
∠
B) =(64+225-144)/240=145/240=29/120
Из треугольника АВМ по теореме косинусов:
АМ²=АВ²+ВМ²-2·АВ·ВМ·сos(
∠
B)
AM²=8²+6²-2·8·6·(29/120)=64+36-23,2=76,8
АМ=16√0,3