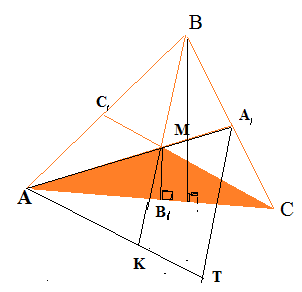
Дан треугольник АВС, АА₁ , ВВ₁, СС₁- его медианы, которые пересекаются в точке М ( см. рисунок)
Отложим отрезок В₁К, равный МВ₁
Четырехугольник АМСК параллелограмм, так как его диагонали в точке В₁ делятся пополам.
Значит
S (Δ AMK)= S (Δ AMB₁) + S(Δ AB₁K)= S(Δ AMB₁)+S(Δ MB₁C)=S(Δ AMC)=1/3 S( Δ ABC)
Треугольник АМС и АВС имеют общее основание АС
ВМ:ВВ₁=2:1медианы в точке пересечения делятся в отношении 2:1, считая от вершины, значит В₁М:В₁В =1:3 и
высота треугольника АМС в три раза меньше высоты треугольника АВС.
Кроме того,

Проведём А₁Т || МК. Тогда треугольники АА₁Т и АМК подобны и АА₁=3/2·АМ= 
Из подобия треугольников получаем

т.е. стороны треугольника АА₁Т равны медианам данного треугольника

Значит площадь треугольника АВС в 4/3 раза больше площади треугольника из медиан.
Площадь треугольника, образованного медианами 3,4, 5 равна 6 кв. см.
Это прямоугольный треугольник 5²=3²+4²
Площадь такого треугольника равна половине произведения катетов.
Площадь треугольника АВС 4/3·6=24/3=8 кв. см