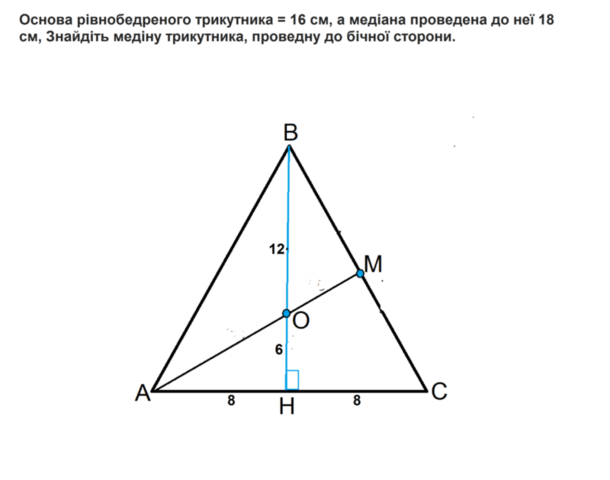
Пусть дан треугольник АВС, АВ=ВС
ВН - медиана ( она же и высота равнобедренного треугольника) к АС и равна 18см
АС=16см
АН=НС=8 см
Проведём из вершины А медиану АМ к боковой стороне ВС.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
ОН=ВН:3=6см
Из прямоугольного треугольника АОН найдем АО по т. Пифагора
АО²=ОН²+АН²=64+36=100
АО=10 см
АО=2/3 медианы АМ ( по свойству точки пересечения медиан)
АМ=10:2*3=15 см