Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 28, а площадь 98.
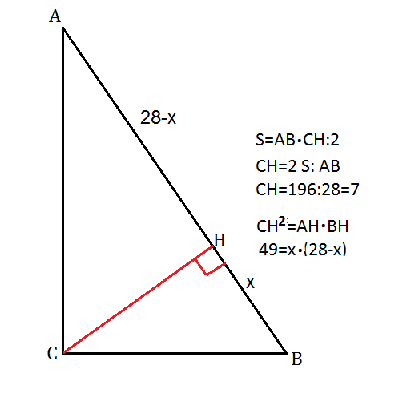
Пусть треугольник будет АВС, С=90º, АВ=18, СН- высота из прямого угла к гипотенузе.
S=AB*CH:2
СН=2S:АВ
СН=196:28=
7
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
СН²=АН*ВН
Пусть ВН=х, тогда АН=28-х.
49=х*(28-х)
х²-28х+49=0
D=588
Решив квадратное уравнение, получим два корня:
х₁
=( 28+√588):2= 14-7√3.
х₂
=( 28-√588):2= 14+7√3
tg A=CH:BH=7:(14+7√3)=≈0,2679
tg B=CH:AH=7:(14-7√3)=≈3,7320
Угол А=artg 0,2679 и равен ≈15º
Угол В=artg 3,7320 и равен ≈75º