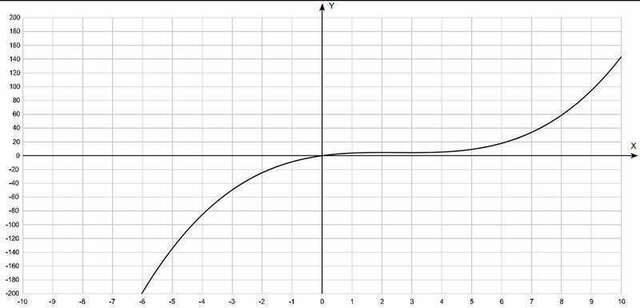
Y=1/3x^3-5/2x^2+6x
решаем уравнение
1/3x^3-5/2x^2+6x=0
x(1/3x^2-5/2x^2+6)=0
x=0
1/3x^2-5/2x^2+6=0
x^2+7,5x+18=0
a=1, b=7,5, c=18
D=b2−4ac=7,52−4·1·18=56,25−72=−15,75
так как D<0,то уравнение не имеет корней<br>у нас один корень кубического уравнения x=0
исследуем функцию на монотонность
производная
y'=(1/3x^3-5/2x^2+6x)'=x^2-5x+6
при x=0 y'=6 положительное число , значит функция
возрастает в промежутке от -∞ до +∞
Вычисление значений функции
y=1/3x^3-5/2x^2+6x
Значение x Значение y
-8 -378.7
-6 -198
-4 -85.3
-2 -24.7
-1 -8.8
0 0
1 3.8
2 4.7
6 18
8 58.7
10 143.3
смотри график ниже