Помогите пожалуйста!Равнобедренная трапеция с основаниями 2 и 3 см и острым углом 60°...

В равнобедренной трапеции проведем высоты из вершин меньшего основания на большее.
Получим Два прямоугольный треугольника и прямоугольник со сторонами 2 см и h ( трапеции)
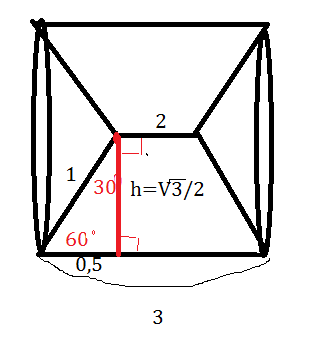
В прямоугольном треугольнике один угол 60⁰, значит второй острый угол 30⁰
Против угла в 30 ⁰лежит катет, длина которого равна (3-2)/2=0,5
Известно, что катет, лежащий против угла в 30° равен половине гипотенузы. Значит гипотенуза ( боковая сторона трапеции) равна 1 см.
По теореме Пифагора найдем высоту трапеции h²=1²-(0,5)²=0,75 =3/4=√3/2

Фигура вращения состоит из цилиндра, радиус основания которого равен h=√3/2 и высота цилиндра равна меньшему основанию трапеции 2 см
И двух конусов с тем радиусом √3/2 и высотой 0,5 см

$V= \pi ( \frac{ \sqrt{3} }{2}) ^{2}\cdot2+2\cdot \frac{1}{3} \pi ( \frac{ \sqrt{3} }{2}) ^{2}\cdot (0,5) = \frac{7 \pi }{4}$
куб ед.