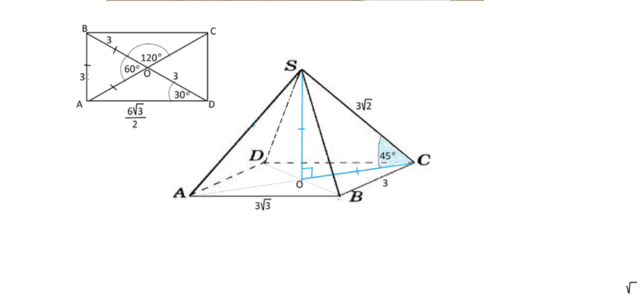
Основание пирамиды-прямоугольник с углом между диагоналями 120° градусов. Все боковые ребра пирамиды равны 3√2 см и наклонены к плоскости основания под углом 45°. Найдите объем пирамиды.
Боковые ребра пирамиды равны и наклонены к плоскости основания под углом 45°, следовательно,
проекции ребер на плоскость основания также равны между собой и равны половинам диагоналей основания
,
а треугольник, образованный высотой SO пирамиды
, половиной OC диагонали и боковым ребром SC - прямоугольный равнобедренный.
Отсюда высота SO пирамиды также равна половине диагонали.
По т. Пифагора или формулы равнобедренного прямоугольного треугольника с=a√2
высота SO пирамиды и
половина диагонали основания равны
3 см.
Основание пирамиды - прямоугольник с углом между диагоналями 120° градусов, значит, второй угол между ними 60°.
Меньшая сторона прямоугольника образует с половинами диагоналей равносторонний треугольник, ⇒
меньшая сторона основания также равна
3 см
Диагональ основания равна
3*2=6 см
Большая сторона основания - катет
, противолежащий углу 60° и равна 6*sin(60°)=
3√3 см
Объем пирамиды равен произведению площади основания на высоту, деленную на 3:
V=Sh
:3
V=3*(3√3)*3
:3=
9√3 см³