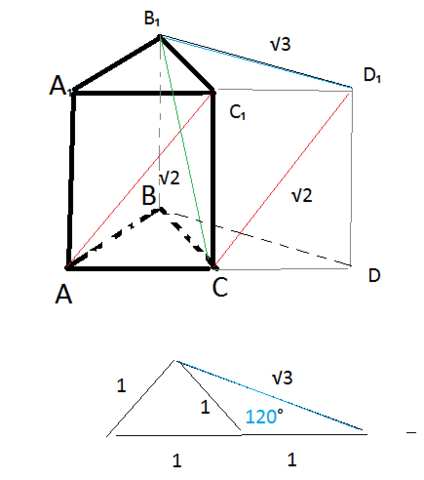
См. рисунок к задаче 36
Продолжим сторону АС за точку С на отрезок СD=1
Из треугольника ВСD
BD²=BC²+CD²-2·BC·CD·cos(
∠ BCD) =1+1-2·1·1·(-1/2)=3
BD=B₁D₁=√3
Угол между АС₁ и В₁С равен углу между СD₁ и В₁С в треугольнике В₁СD₁
B₁C=CD₁=√2
По теореме косинусов:
(√3)²=(√2)²+(√2)²-2√2√2 сos∠ B₁CD₁ ⇒сos∠ B₁CD₁ =1/4