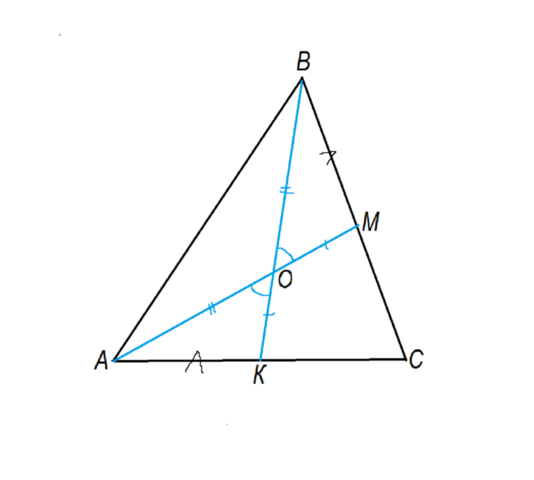
Сделаем рисунок.
Обозначим вершины треугольника А, В, С, середины сторон, к которым проведены медианы, К на АС, М-на ВС, точку их пересечения - О.
Медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.
Следовательно, ВО=АО, а оставшиеся части ОМ=ОК.
Углы при О треугольников ВОМ и КОА равны как вертикальные. Треугольники АОК и ВОМ равны по двум сторонам и углу между ними. АК=ВМ. Но эти отрезки - половины АС и ВС.
Следовательно, АС=ВС, и треугольник АВС, в котором две медианы равны, равнобедренный.