Биссектрисы углов A и C трапеции ABCD пересекаются в точке P, а биссектрисы углов B и D —...

Question

Биссектрисы углов A и C трапеции ABCD пересекаются в точке P, а биссектрисы углов B и D — в точке Q, отличной от P. Докажите, что если отрезок PQ параллелен основанию AD,
то трапеция равнобокая.

Comments

У меня появилась гениальная идея :)

---

В общем если там на продолжении оснований повозить параллельно боковые стороны то можно добится что все 4 бессектрисы пересекутся в 1 точке. ТО около полученной трапеции (боковые стороны которой анологичны старой) Можно описать окружность. То она равнобокая. То и искомая трапеция равнобокая :) Завтра напишу.

---

Ай нет это ж для вписанной окружности перепутал :) ТОгда идея не сработает :)

Answer 1

Я  даже не знаю как  мне обьяснить пошагово решение этой задачи,но  я попробую. Потому что метод довольно  кондовый. 
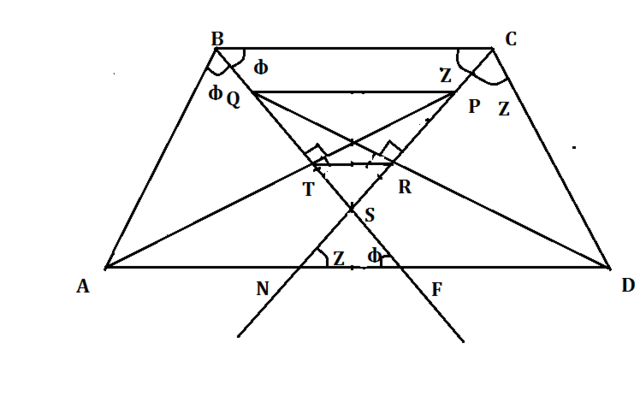
Обозначенные углы равны как   внутренние накрест лежащие и  углы бьющиеся  бессектрисой. Откуда   треугольники ABF и CND   равнобедренные.  То  бессектрисы  AT и DR медианы и высоты.(BT=TF) (CR=RN) Треугольники BSC и NSF   подобны по 2   углам.
BS/SF=CS/SN  поиграв с отношениями   получим что
ТS/SF=RS/SN То   треугольники  TSR  и  NSF подобны по 2 пропорциональным сторонам и равным  вертикальным углам между ними. То   углы крест накрест равны. То  TR  параллельно  NF.
ТR   параллельно  QP (QTRP-трапеция). Известным фактом   является,что если диагонали трапеции состовляют с  ее  боковыми  сторонами равные   углы (в  данном случае прямые) То  она равнобочная.
ТО есть  угол  P=Q то  из   соответственных   углов Ф=Z   ,то   углы  D=A.  То   наша трапеция   равнобочная
ЧТД

---

Comments

Это короткое решение. Если нужно могу пояснить как именно я (Играл с отношением)