Первый способ
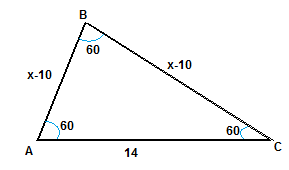
Дан угол 60 градусов и сторона 14см. две другие углы треугольника также будут равны по 60 градусов. Следовательно, треугольник - равносторонний.
У равностороннего треугольника все стороны равны: АВ = ВС = АС = 14 см.
Периметр треугольника равна сумме всех сторон
P = AB+BC+AC=14+14+14=42 см.
Второй способ
Пусть две другие стороны будут по (х-10) см и угол между ними 60 градусов.
по т. Косинусов имеем

Следовательно, две другие стороны равны - (x-10)=(24-10)= 14 см.
Р=AB+BC+AC=14+14+14 = 42 см.
Ответ: 42 см.