В трапеции ABCD, основание BC = 4, AD = 64, диагональ BD =16. Доказать что треугольники...

Question

В трапеции ABCD, основание BC = 4, AD = 64, диагональ BD =16. Доказать что треугольники CBD и ADB подобны

Answer 1

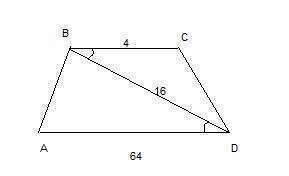
Треугольники CBD и ADB подобны по второму признаку подобия: две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны.
В нашем случае углы CBD и ADB равны как накрест лежащие углы при пересечении двух параллельных прямых ВС и AD секущей BD.
Для соответственных сторон треугольников можно записать:
ВС : BD = BD : AD, 4 : 16 = 16 : 64 = 1 : 4. Стороны, между которыми заключены равные углы, пропорциональны. 

---

Comments

ABCD - трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это накрест-лежащие углы для параллельных прямых AD и BC).
Рассмотрим отношения сторон:
BC/BD=4/16=1/4
BD/AD=16/64=1/4
Тогда по второму признаку подобия треугольников, треугольники CBD и ADB подобны.