Найдем вершину параболы у = –х2 + 4mх – m
х=-4m/-2=2m
y=- 4m^2+8m^2-m=4m^2-m
найдем вершину параболы у = х2 +2mх – 2
х=-2m/2=-m
y=m^2-2m^2-2=-m^2-2
(х находится по формуле x=-b/2a, а потом значение у подставляется уравнение )
т.к. нам надо найти вершину расположенную по одну сторону от ОСИ Х, то произведение координаты у одной и другой параболы должно быть положиельным.(т.к. если они оба отрицательны, то их произведение положительно, а если они оба положительны, то произведение тоже положительно).
получаем следующее неравенство:
(4m^2-m)(-m^2-2)>=0
-m^2-2 всегда отрицательно при любом значении m, потому что -(m^2)-отрицательно, и -2 тоже отрицательно.
соответственно , чтобы произведение (4m^2-m)(-m^2-2) было отрицательным надо, чтобы (4m^2-m) было отрицательно
получаем следующее неравенство 4m^2-m<=0<br>2m(2m-1)=0
2m=0, m=0
2m-1=0; m=0,5
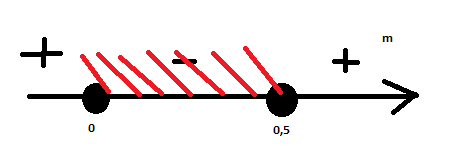
наносим на координатную прямую и по методу интервалов получаем(смотри рисунок)
получаем:
m[0;0,5]
Ответ: [0;0,5]