Задача простая, но с ее решением иногда путаются, т.к. конус - перевернутый.
И на глаз видно, что объем нижней - заполненной - части конуса гораздо меньше пустой.
Объем конуса ( и стоящего на основании, и перевернутого в виде бокала) находят по формуле
V=Sh:3.
То есть площадь основания (круга), умноженную на высоту, делят на 3.
( Так же, как в пирамиде)
.Если рассмотреть осевое сечение конуса, увидим, что это равнобедренный треугольник.
При этом высота меньшего треугольника ( высота меньшей части конуса с жидкостью) по условию в два раза меньше высоты всего конуса.
Отсюда отношение линейных размеров подобных треугольников СКМ и АВС равно 1:2, и коэффициент подобия k=1/2
Отсюда и радиус конуса АВС равен двум радиусам конуса КМС
Все это - немного теории в качестве объяснения.
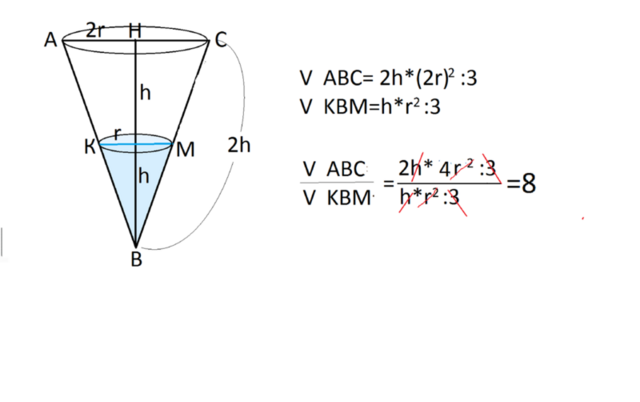
В приложенном рисунке даны вычисления, сделанные с помощью формул.
В данной задаче можно дать короткое решение, применив свойство отношений объемов подобных фигур:
Объемы подобных фигур относится как куб коэффициента их подобия.
Пусть объем заполненной части конуса будет V1,
а объем всего конуса - V2
V1:V2= k³= (1/2)³=1/8
Следовательно, объем всего конуса в 8 раз больше заполненной части и равен 8*25=200(мл)
Чтобы заполнить конус жидкостью, необходимо добавить
200-25=175 (мл)
------------
[email protected]