1) Неравенство треугольника. Во всяком треугольнике каждая сторона меньше суммы двух других:
a < b +c
b < a + c
c < a + b
Подставим а = 15, с = 18
15 < b + 18
b < 15 + 18
c < 15 + b
Из этих неравенств и получим оценку для b
3 < b < 33
Теорема Пифагора может быть применена в двух случаях
Либо
15² + 18² = b² ⇒ b =√549=3√61
либо
15²+ b²=18² ⇒ b²= 324-225 b²=99 ⇒ b =√99
Ответ. 3 < b < 33
треугольник прямоугольный при b =3√61 или b =√99
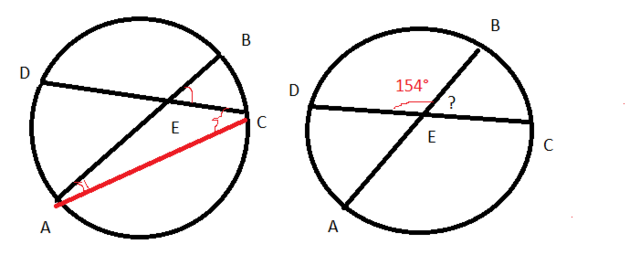
2) Угол между пересекающимися хордами равен полусумме дуг, на которые опирается этот угол и ему вертикальный. ( см. рис.1)
Доказательство этого свойства:
Угол ВЕС -внешний угол треугольника АЕС равен сумме двух других углов этого треугольника с ним не смежных
∠ВЕС= ∠А + ∠С = 1/2 дуги BC + 1/2 дуги AD
См. рис. 2
Решение задачи .
∠ ВЕС = 180° - ∠ АЕС =180° - 154°= 26°
По доказанному свойству
∠ВЕС= ∠А + ∠С = 1/2 дуги BC + 1/2 дуги AD
Пусть дуга AD содержит х°, тогда дуга ВС содержит 0,3х°
26°= 1/2 ·х° + 1/2 ·0,3х°==1/2 (1,3 х°)
1,3х°=52°
х°= 52° : 1,3
х= 40°
Значит дуга AD содержит 40°, а дуга ВС содержит 0,3· 40°=12°
Ответ. Дуга AD содержит 40°, а дуга ВС содержит 12°