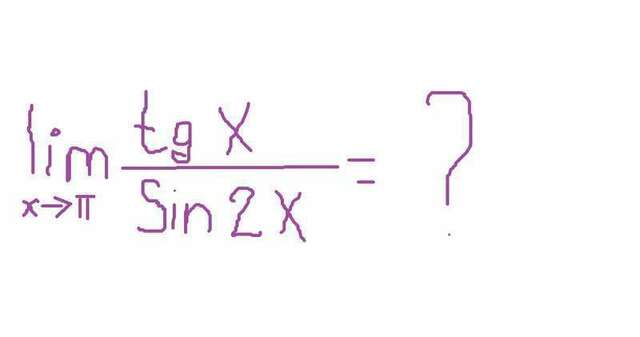Пожалуйста, помогите найти предел! Меня интересует решение, ответ есть.Большое спасибо...

0 голосов
40 просмотров

Пожалуйста, помогите найти предел! Меня интересует решение, ответ есть.
Большое спасибо тем, кто откликнется ^_^

Решить нужно двумя способами:
1- Полагая х = 2+L (L - в смысле угол альфа)
2- Разложить знаменатель на мноители

Объясните мне, безнадежной, в чем разница

image
Математика (84 баллов) | 40 просмотров
0

Сделать замену переменной (х-pi)=t. Затем применить формулы приведения и 1-й замечательный предел или эквивалентность

оставил комментарий (414k баллов)
Дано ответов: 2
0 голосов
Правильный ответ

Lim(tgx/sin2x)=lin(sinx/2sinxcos²x)=lin(1/2cos²x)=1/2
0 голосов
1) \lim_{x \to \pi } \frac{tgx}{sin2x} =[x- \pi =t, x=t+ \pi ]= \lim_{t \to0} \frac{tg(t+ \pi )}{sin(2t+2 \pi )}= \\ \lim_{t \to 0} \frac{tgt}{sin2t} = \lim_{t \to0}( \frac{tgt}{2t} \cdot \frac{2t}{sin2t}) = \frac{1}{2} , \\ 2)\lim_{x \to \pi } \frac{tgx}{sin2x} =[x- \pi =t, x=t+ \pi ]= \lim_{t \to0} \frac{tg(t+ \pi )}{sin(2t+2 \pi )}= \\ \lim_{t \to 0} \frac{tgt}{sin2t} = \lim_{t \to0}( \frac{tgt}{2sintcost} ) = \\ = \lim_{t \to0}( \frac{tgt}{t} \frac{t}{2sint} )\ =\frac{1}{2}
cos0=1
(414k баллов)
Похожие задачи