В прямоугольной трапеции ABCD высота AB равна сумме оснований AD и BC. Биссектриса угла...

Question

В прямоугольной трапеции ABCD высота AB равна сумме оснований AD и BC. Биссектриса угла ABC пересекает сторону CD в точке K. В каком отношении эта точка делит CD?

Answer 1

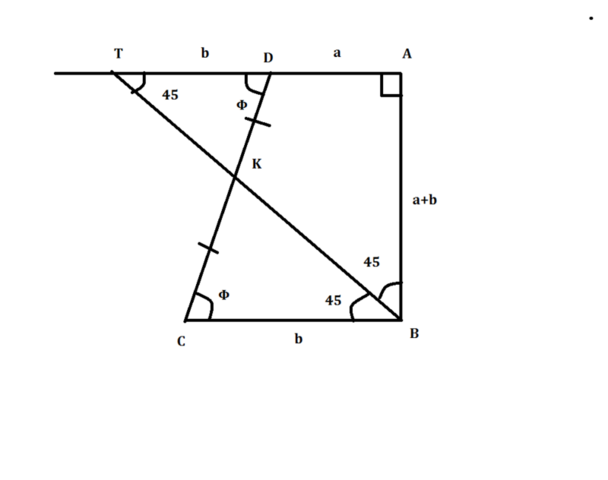
В  целом детская задачка:
Продолжим верхнее  основание  и биссектрису до  пересечения  в точке T.  Указанные углы равны  как внутренние накрест лежащие  и углы деленные биссектрисой.  То треугольник  BAT-равнобедренный.
Таким образом  AT=a+b   TD=BC=b. Таким  образом треугольники  ТKD и CBK  равны по  стороне и двум прилежащим  углам.   То выходит  что     CK=KD
 Ответ:1:1                           

---