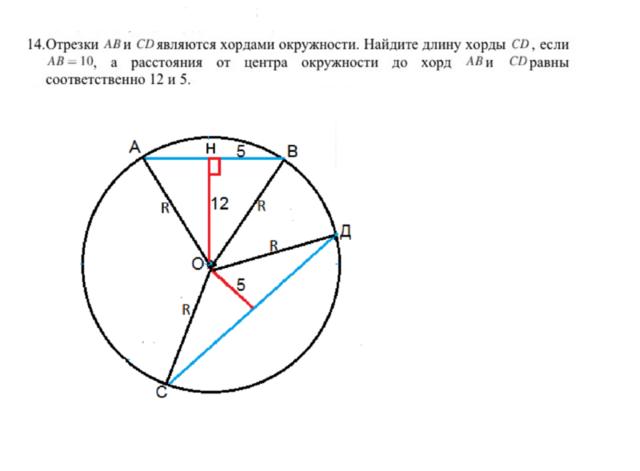
Отрезки АВ и СD являются хордами окружности. Найдите длину хорды СD, если АВ=10, а расстояние от центра окружности до хорд АВ и CD равно соответственно 12 и 5.
Сделаем рисунок.
Соединим центр окружности с концами хорд.
Проведем в получившихся равнобедренных треугольниках ( их стороны - радиусы) высоты - они и есть расстояния от центра до хорд, т.к. расстояние находят перпендикулярными отрезками.
Треугольник АОВ высотой ОН поделен на два прямоугольных с катетами 5 и 12. Можно без вычисления узнать, что гипотенуза ( радиус) равна 13, т.е. это отношение одной из Пифагоровых троек. ( можно проверить)
В треугольнике АОD высота равна 5 и делит его на два прямоугольных с гипотенузой 13, катетом 5 и вторым, равным половине СD.
Здесь также получился треугольник из той же Пифагоровой тройки.
Половина CD=12, a вся хорда
CD=12*2=
24