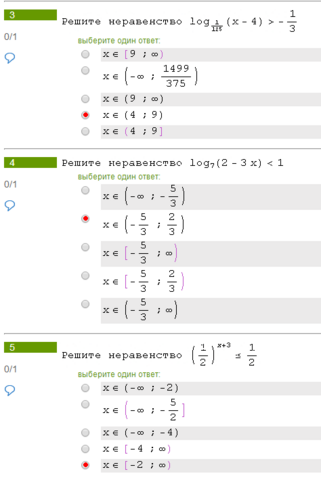
3) -1/3 = log(1/5)(∛5)
log(1/125)(x - 4) = (1/3)*log(1/5)(x - 4) = log(1/5)∛(x - 4)
log(1/5)∛(x - 4) > log(1/5)(∛5)
∛(x - 4) < ∛5
x - 4 < 5, x < 9
ОДЗ: x - 4 > 0, x > 4
Объединяя решения: 4 < x < 9<br>Ответ: x∈(4; 9)
4) 1 = log7(7)
log7(2 - 3x) < log7(7)
2 - 3x < 7, -3x < 5, x > -5/3
ОДЗ: 2 - 3x > 0, 3x > -2, x < 2/3
Ответ: x∈(-5/3; 2/3)
5) (1/2)^(x+3) ≤ (1/2)^1
x + 3 ≥ 1, x ≥ -2
Ответ: x∈[-2; +бесконечность)