Замена : √x=t>=0
t⁴-4*t²-32=4*(t²-8)*t
t⁴-4*t³-4*t²+32*t-32=0
Для того чтобы уменьшить коэффициенты и облегчить отбор заменим:
t=2*u u>=0
16*u⁴-32*u³-16*u²+64*t-32=0
u⁴-2*u³-u²+4*u-2=0
Не трудно догадаться u₁=1
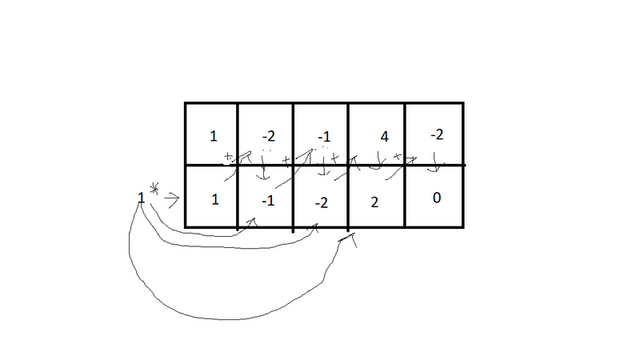
Делим по схеме горнера этот многочлен на (u-1)
Cмотрите рисунок:
Итак:
(u-1)*(u³-u²-2*u+2)=0
(u-1)(u²*(u-1) -2*(u-1))=0
(u-1)²*(u²-2)=0
(u-1)² * (u-√2)*(u+√2)=0
u₁=1 u₂=√2 u₃=-√2 <0 не подходит.<br>t₁=2 t₂=2*√2
x₁=4
x₂=8
Ответ:x₁=4 ; x₂=8