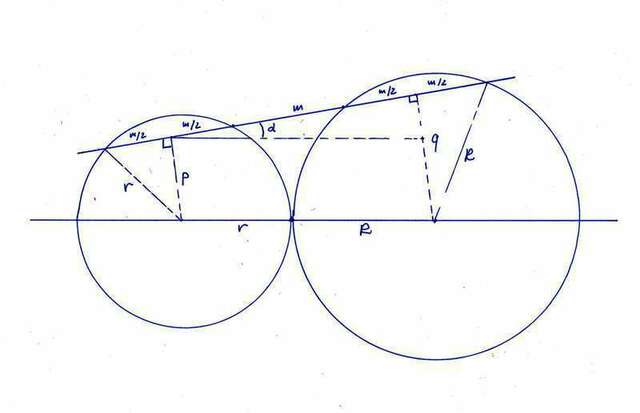
См. ПЕРВЫЙ чертеж. На нем все обозначения.
q^2 = R^2 - (m/2)^2;
p^2 = r^2 - (m/2)^2;
Отсюда
(2*m)^2 + (q - p)^2 = (R + r)^2; (это просто теорема Пифагора)
4*m^2 + q^2 + p^2 - 2*q*p = R^2 + r^2 + 2*R*r;
4*m^2 + R^2 + r^2 - m^2/2 - R^2 - r^2 - 2*R*r = 2*q*p; (свожу подобные и делю на 2);
(7/4)*m^2 - R*r = q*p; (это возводится в квадрат);
(49/16)*m^4 - 2*(7/4)*m^2*R*r + R^2*r^2 = (R^2 -m^2/4)*(r^2 - m^2/4) =
= R^2*r^2 - (1/4)*m^2*(R^2 + r^2) + m^2/16; (ясно, что свободные от неизвестного m слагаемые выпадают, и степень понижается :));
3*m^2 = (7/2)*R*r - (R^2 + r^2)/4;
Собственно, это ответ. Его можно "переписывать" в каких-то иных формах, например, так
m = (√3/6)*√(16*R*r - (R + r)^2);
сути это не меняет.
Почему эта задача вызвала такие моральные затруднения, я не понимаю.
Арифметику проверяйте! :)
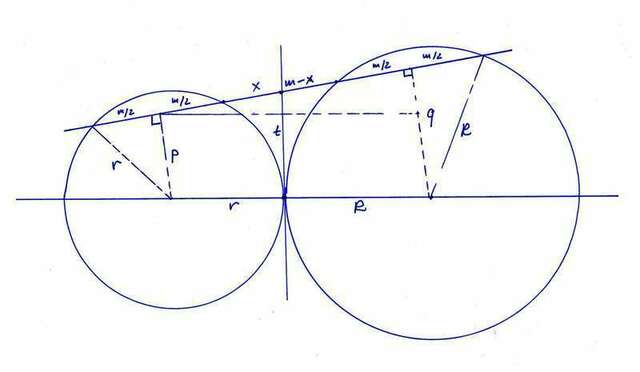
Мне захотелось показать несколько простых ЧУДЕС, которые зарыты в этом условии. См. ВТОРОЙ рисунок, он немного отличается от первого. Семь отличий искать не надо :). Проведена общая внутренняя касательная до пересечения с прямой. Она делит средний (из трех равных) отрезок на части x и m - x; отрезок касательной t;
Ясно, что x*(x + m) = t^2 = (m - x)*(m - x + m);
откуда легко найти x = m/2;
то есть общая внутренняя касательная делит средний отрезок пополам.
Это уже НЕЧТО, но есть и дальше :)
r^2 + t^2 = p^2 + (x + m/2)^2 = r^2 - m^2/4 + m^2;
t^2 = (3/4)^m^2;
t = m*√3/2;
к сожалению, это не сильно помогает в поиске m :);