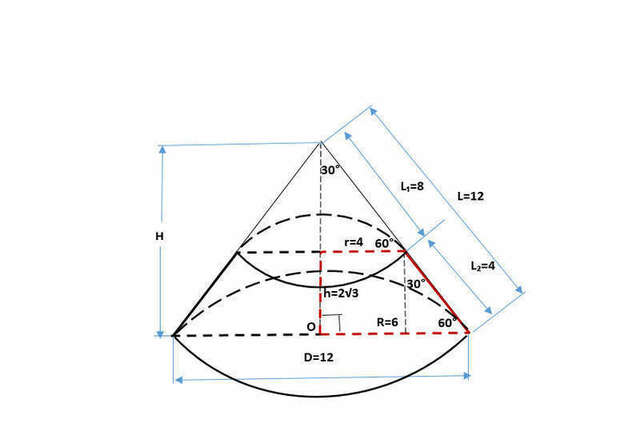
Вращая трапецию(красная на рис.)вокруг стороны h, получим усечённый конус.Если продлим боковые стороны трапеции , получим прямоугольный треугольник, вращая который получим сам конус с высотой H и диаметром основания D=12.
Осевое сечение усечённого конуса - равнобедренная трапеция с основаниями 4*2=8 и 6*2=12
L - образующая конуса(гипотенуза в прямоугольном треугольнике)
R - радиус основания конуса(сторона прямоугольного треугольника , она же нижнее основание прямоугольной трапеции)
R = 1/2 гипотенузы L, лежит напротив угла 30°поэтому:
L/2=R; L/2=6; L=12
L₁- образующая верхнего конуса
r - - радиус основания верхнего конуса(сторона прямоугольного треугольника , она же верхнее основание прямоугольной трапеции)
r= 1/2 гипотенузы L₁, лежит напротив угла 30°поэтому:
L₁/2=r; L₁/2=4; L₁=8
L₂-боковая сторона прямоугольной трапеции , а так же равнобедренной трапеции(сечение усечённого конуса), она же гипотенуза прямоугольного треугольника с высотой h.
L₂=L-L₁=12-8=4
h=L₂*sin60°=4*√3/2=2*√3
S₁ - Площадь осевого сечения,это площадь трапеции с высотой h=2*√3 и основаниями D=12 и 2*r=8
S₁= 2*√3(12+8)/2=20*√3
S₂ -боковая площадь усечённого конуса= разности боковых поверхностей конусов с образующими L и L₁
S₂=π*R*L-π*r*L₁=π*(R*L-r*L₁)=π*(6*12-4*8)= 40*π
S-полная площадь усечённого конуса=сумме площадей верхнего и нижнего оснований(окружности с радиусами R и г) плюс площадь боковой поверхности(развёртки) усечённого конуса.
S = S₂+π*R²+π*r²=40*π+6²*π + 4²*π= 92*π
Смотри рисунок ниже