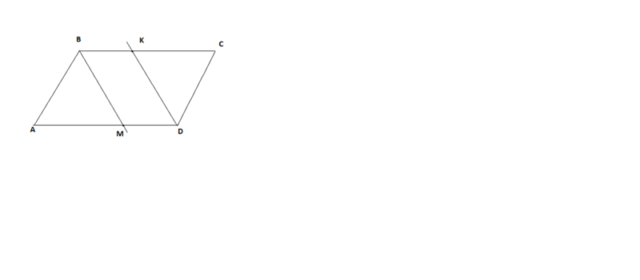
1. АВ=АМ.
CD=CK
Т.к. ABCD - параллелограмм, то АВ=CD. Но мы выше вывели, что АВ=АМ, а CD=CК, значит
АМ=СК
Треугольники АМВ и CKD получаются равны по двум сторонам и углу между ними: АВ=CD, АМ=СК, углы А и С равны как противоположные углы параллелограмма.
2. ВК=ВС-СК, DM=AD-АМ. Поскольку ВС=AD, а СК=АМ (как равные соответственные стороны равных треугольников АМВ и CKD), то ВК=DM. Эти отрезки лежат на параллельных сторонах ВС и AD, значит, они также параллельны. Значит, BKDM - параллелограмм (две стороны равны и параллельны), следовательно, ВМ II DK.