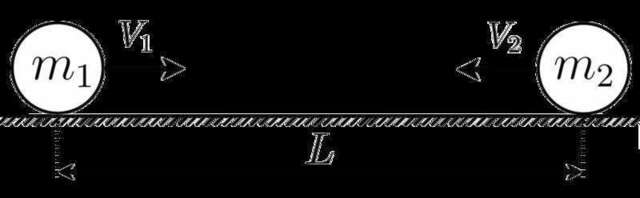
Экспериментатор Глюк решил исследовать центральное столкновение шариков. ** гладкой...

Question

91 просмотров

Экспериментатор Глюк решил исследовать центральное столкновение шариков. На гладкой горизонтальной поверхности стола на расстоянии L=4 м друг от друга он расположил два маленьких шарика массами m1=230 г и m2=350 г. Далее он сообщил им скорости V1=0,8 м/с и V2=0,2 м/с, одновременно нажав на кнопку «старт» секундомера. Они сблизились, абсолютно упруго столкнулись и начали удаляться друг от друга. Что показал секундомер в момент, когда расстояние между шариками снова стало равным L? Ответ выразить в с, округлив до целых.

Физика oselka21_zn (334 баллов) 20 Март, 18 | 91 просмотров

Дан 1 ответ

Zakadym_zn · Answer 1 · 2018-03-20T05:43:04+0000

Для начала найдем время за которое они столкнуться его можно найти из формулы $x=x_0+v_0t+ \frac{at^2}{2}$ так как ускорения у нас равно 0, то она преобразится в такую $x=x_0+v_0t$ теперь надо приравнять координаты 1го и 2го шаров(это и будет место столкновения) $x_1=x_2$ тогда если взять начальную координату одного шара за 0 а координату другого за 4, и учесть что 2 шар катится назад. что значит его скорость отрицательна можно записать такое выражение $x_0_1+v_0_1t=x_0_2+v_0_2t$ откуда время будет равно $t= \frac{x_0_1-x_0_2}{v_0_2-v_0_1}= \frac{0-4}{-0,2-0,8}=4$ это время за которое они столкнуться.
Теперь найдем их скорости в момент после столкновения, они будут равны $v_1= \frac{2m_2v_0_2+v_1(m_1-m_2)}{m_1+m_2}=0,076$ и $v_2= \frac{2m_1v_0_1+v_2(m_2-m_1)}{m_1+m_2}=0,676$ теперь нам надо найти время за которое они удалятся друг от друга и это будет $t= \frac{S}{v_1+v_2}= \frac{4}{0,076+0,676}=5,31$ плюс то время за которое они сближались и у нас получается что общее время равно 9,31