Высота сн прямоугольного треугольника авс, опущенного ** гипотенузу ав, разбивает этот...

Question

Высота сн прямоугольного треугольника авс, опущенного на гипотенузу ав, разбивает этот треугольник на два прямоугольных треугольника сан и свн, периметры которых равны соответственно 5 и 12. найдите периметр треугольника авс.

Answer 1

1) ΔАСН подобен ΔСВН⇒ ВС/AC=12/5,  пусть х-коэф. пропорциональности, тогда ВС=12х, АС=5х.
2) По т. Пифагора АВ=13х, СН=АС·ВС/АВ=60x/13
3) Получим уравнение: 5х+12х+13х+120х/13=5+12
510x=17·13
x=13/30
P(ABC)=30x=13

Comments

всем огромное спасибо, не надеялась на столь быстрый ответ

Answer 2

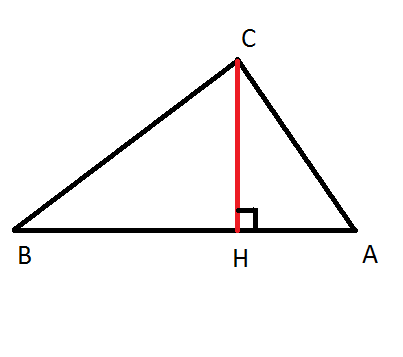
Треугольники ВСН и АСН подобны, их сходственные стороны относятся как периметры
ВС:АС=12:5  ⇒  ВС=12·АС/5
Пусть АС=х, тогда ВС=12х/5, по теореме Пифагора
АВ²=АС²+ВС²=х²+144х²/25=169х²/25
АВ=13х/5

Так как площадь прямоугольного треугольника равна половине произведения катетов и половине произведения гипотенузы на высоту, то
ВС·АС=АВ·СН
12х²/5=13·СН·х/5
12х=13СН
СН=12х/13

Из условия
ВС+СН+ВН=12
АС+СН+АН=5  ⇒  ВС+СН+ВН+АС+СН+АН=17 ⇒ Р=17-2·СН

или
12х/5 +12х/13 + ВН=12
х+12х/13+АН=5
складываем
12х/5 +12х/13+ВН + х +12х/13+ АН=17, но АН+ВН=АВ=13х/5
12х/5 +24х/13+х + 13х/5=17,
х=13/6
СН=12х/13=12·13/6·13=2
Р= 17-2·СН=17-2·2=13
Ответ. P(Δ АВС) =13 см

---

Comments

а ответ в учебнике 13(((((

---

всё равно спасибо большущее)))

---

да, в последней строчке неверно.Сейчас исправлю