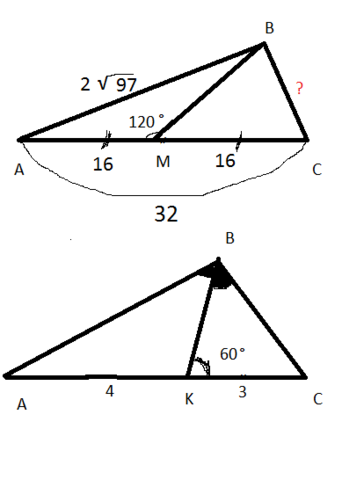
1) AM=MC=16 см. Так как медиана делит противоположную сторону пополам (см рисунок)
Из треугольника АВМ по теореме косинусов:
АВ²=АМ²+МВ²-2АМ·МВ·cos 120°
АВ=2√97, АМ=16, ВМ=х
Получаем уравнение:
4·97=16²+х²-2·16·х·(-1/2)
х²+16х-132=0
D=256+4·132=4(64+132)=4·196=(2·14)²=28²
x=(-16-28)/2<0 или х=(-16+28)/2=12/2=6<br>ВМ=6
Из треугольника ВМС по теореме косинусов
ВС²=ВМ²+МС²-2ВМ·МС·cos 60°=6²+16²-2·6·16·(1/2)=196=14²
ВС=14
Ответ. ВС=14- третья сторона треугольника равна 14 см
2) Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника:
АК: КС= АВ: ВС
значит
АВ:ВС=4:3
или
АВ=4х, ВС=3х
По теореме косинусов из треугольника ВКС:
ВС=3х, КС=3, ∠ВКС=60°
ВС²=ВК²+КС²-2·ВК·КС·сos 60°
(3x)²=BK²+9-2·BK·3·(1/2)
9x²=BK²-3·BK+9 ( * )
По теореме косинусов из треугольника AВК:
AВ=4х, AК=4, ∠ВКA=120°
AВ²=AК²+BK²-2·AК·BК·сos 120°
(4x)²=16+BK²-2·BK·4·(-1/2)
16·x²=BK²+4·BK+16 ( ** )
Решаем систему двух уравнений ( * ) и ( ** )с двумя неизвестными х и ВК
заменим х² в уравнении ( ** ) на выражение (BK²-3·BK+9)/9 из ( *):
16·(BK²-3·BK+9 )/9=BK²+4·BK+16 - умножим уравнение на 9
16·ВК² -48·ВК+16·9=9·ВК²+36·ВК+9·16
7·ВК²-84·ВК=0
7·ВК·(ВК-12)=0
ВК-12=0
ВК=12
Ответ. биссетриса равна 12