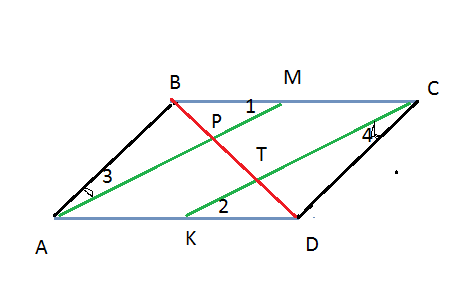
Обозначим точку пересения АМ с BD - точка Р
Выберем точку К на стороне AD. АК=КD=ВМ=МС
Проведем CK.
СК || AM, так как
треугольники АВМ и КСD равны по двум сторонам и углу между ними ( АВ=СD и ВМ=КD, угол В равен углу D)
из равенства треугольников следует равенство углов (угол 1 равен углу 2, угол 3 равен углу 4), но и смежные к ним тоже равны, поэтому внутренние накрест лежащие углы равны, прямые параллельны
Точка пересечения СК с BD - точка Т
По теореме Фалеса
Из треугольника АРD:
АК=KD, значит и РТ=ТD
Из треугольника ВТС:
ВМ=МС, значит и ВР=РТ
ВР=РТ=РD
ВР:PD=1:3