Одна из формул площади треугольника
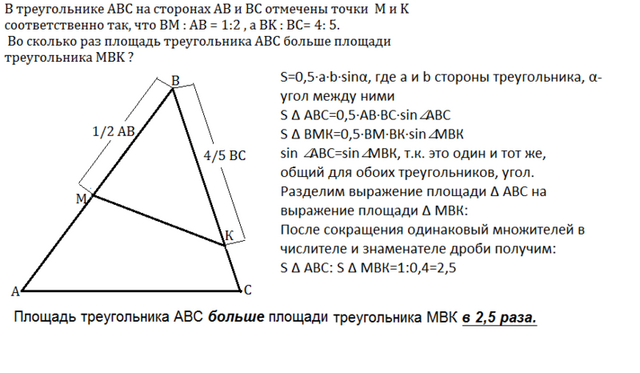
S=0,5·a·b·sinα, где а и b - стороны треугольника, α- угол между ними
S ∆ АВС=0,5·АВ·ВС·sin∠АВС
S ∆ ВМК=0,5·ВМ·ВК·sin∠MBК
sin∠АВС=sin∠MBК, т.к. это один и тот же, общий для обоих треугольников, угол.
Разделим выражение площади ∆ АВС на выражение площади ∆ МВК:
После сокращения одинаковых множителей в числителе и знаменателе дроби получим:
S ∆ АВС: S ∆ МВК=1:0,4=2,5
Площадь треугольника АВС больше площади треугольника МВК
в 2,5 раза.