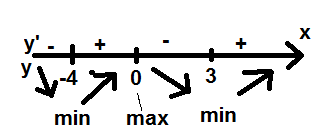логарифмы опускаем, т.к. основания равны:

0, \; \; 3x+0.5>0 \\ => \; kornei net" alt="3x+0,5=x-2; \; \; 2x=-2,5; \; \; 2x=-\frac{5}{2}; \; \; x= -\frac{5}{4} =-1,25 \\ ODZ: \; x-2>0, \; \; 3x+0.5>0 \\ => \; kornei net" align="absmiddle" class="latex-formula">
чтобы найти точки минимума и точки максимума, нужно взять производную и приравнять к нулю.

дальше фото
ответ: 0