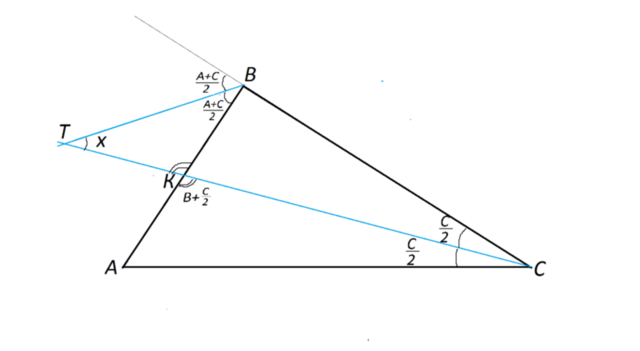
Докажите, что биссектриса внешнего угла при вершине В и биссектриса угла С треугольника АВС пересекаются под углом, равным 1/2 ∠ А.
---------
Сделаем рисунок, обозначим точку пересечения биссектрис буквой Т, точку пересечения биссектрисы угла С со стороной АВ буквой К.
Внешний угол при вершине В равен сумме углов А и С (по свойству внешнего угла).
Биссектриса внешнего угла треугольника делит его на два угла, каждый из которых равен по (А+С):2
Рассмотрим треугольник АКС.
В нем угол при вершине С равен половине угла С исходного треугольника АВС и равен С/2
Угол АКС равен углу В+С/2 ( если от одного угла отнялось, то к другому столько же прибавилось, т.к. угол А остался без изменения)
т.е.
А+(В+С/2)+С/2=180°
В треугольнике ТВК угол при В равен (А+С):2
угол ТКВ=АКС и равен В+С/2
Угол при Т пусть равен х
Выразим сумму углов этого треугольника выражением
(А+С):2+В+с/2+х=180°
Поскольку сумма углов любого треугольника одинакова (180°), приравняем суммы углов треугольников ТВК и АВС
(А+С):2+В+с/2+х=А+В+С
А+С+2В+С+2х=2А+2В+2С
2х=А
х=А/2
что и требовалось доказать.
------
[email protected]