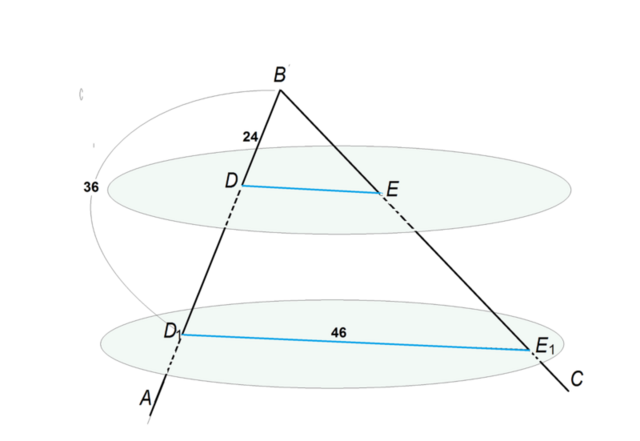
Из свойств параллельных плоскостей:
1)Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Соединим Д₁ и Е₁.
Получим треугольник Д₁ВЕ₁
Плоскость, в которой лежит треугольник Д₁ВЕ₁, пересекает плоскости α и β
по параллельным прямым ДЕ||Д₁Е₁
2)Параллельные плоскости рассекают стороны угла на пропорциональные части.⇒
Треугольники ВДЕ и ВД₁Е₁ подобны.
В них В - общий угол, а углы при ДЕ и Д₁Е₁ равны по свойству углов при параллельных прямых и секущей.
Следовательно,
ВД₁:ВД=Д₁Е₁:ДЕ
36:24=46:ДЕ
36ДЕ=24*46 Сократим обе стороны уравнения на 12:
3ДЕ=8*46
ДЕ=15 ¹/₃
(Возможно, в записи условия опечатка, и тогда, если Д₁Е₁=45,
отрезок ДЕ= 15)