Дан квадрат ABCD вершины A и D которого лежат ** некоторой окружности , а две другие **...

Question

Дан квадрат ABCD вершины A и D которого лежат на некоторой окружности , а две другие на касательной к этой окружности. Через центр окружности проведена прямая параллельная AD. В каком отношении ( считая от вершины А ) эта прямая делит сторону AB???

Answer 1

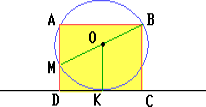
Пусть A и B — вершины квадрата ABCD, лежащие на окружности радиуса R и центром O, D и C — на касательной, проведённой к окружности в точке K, M — точка пересечения окружности со стороной AD. Поскольку BAM = 90o, то MB — диаметр окружности, а т.к. OK — средняя линия трапеции MDCB, то = OK.

Обозначим через x сторону квадрата. Из уравнения = R находим, что MD = 2R - x. Тогда

AM = x - (2R - x) = 2x - 2R.

По тереме Пифагора

AB2 + AM2 = BM2, или x2 + (2x - 2R)2 = 4R2.

Из этого уравнения находим, что x = . Следовательно, диагональ квадрата равна .

---