B3-С2Баллами не обижу (-_-)Заранее спасибо !)

Question

Дан 1 ответ

Правильный ответ

$1)\overrightarrow{n}= \frac{2}{5}\overrightarrow{a}- \frac{2}{3}\overrightarrow{b}}- \frac{3}{4}\overrightarrow{a}+ \frac{3}{2}\overrightarrow{b}=\\=-\frac{7}{21}\overrightarrow{a}+ \frac{5}{6}\overrightarrow{b}}$
$\overrightarrow{m}= 21\overrightarrow{a}-50\overrightarrow{b}$
Далее находим коэффициент пропорциональности
$- \frac{7}{20}k=21\Rightarrow k=-60, \\ \frac{5}{6}(-60)=-50$
верно
$\overrightarrow{m}=-60\overrightarrow{n}.$
2) По правилу треугольника
$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+ \frac{1}{2}\overrightarrow{BC}= \\ =\overrightarrow{AB}+ \frac{1}{2}(\overrightarrow{AC}-\overrightarrow{AB})= \\ = =\overrightarrow{a}+ \frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})= \\ = \frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})$
$\frac{1}{3} \overrightarrow{AD}) = \frac{1}{6}(\overrightarrow{a}+\overrightarrow{b})$
3)
$|\overrightarrow{AB}+\overrightarrow{AD}-\overrightarrow{DC}-\overrightarrow{OD}|= \\ = |\overrightarrow{AC}}+\overrightarrow{CD}-\overrightarrow{OD}|= \\ |\overrightarrow{AD}}+\overrightarrow{DO}|=|\overrightarrow{AO}|= \frac{1}{2}|\overrightarrow{AC}|= \frac{ \sqrt{a ^{2}+b ^{2} } }{2}$
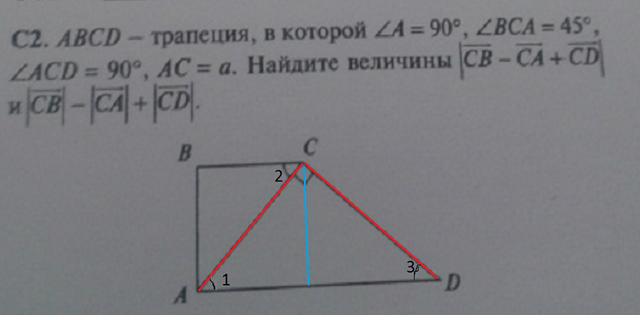
4) Угол BCD равен 45°+90°=135°, сумма углов прилежащих к одной стороне равна 180°, поэтому угол CDA= 45°= ∠ 3
∠ 1= ∠ 2 - внутренние накрест лежащие при параллельных прямых
∠ 1= ∠ 2= ∠ 3= 45°

Проведем высоту СК
Из прямоугольных равнобедренных треугольников
АСD: АС=СD=а ⇒ AD= а√2 ⇒АК = КD = BC = AB = a√2/2
$|\overrightarrow{CB}-\overrightarrow{CA}+\overrightarrow{CD}|=|\overrightarrow{CB}+\overrightarrow{AC}+\overrightarrow{CD}|= \\ =|\overrightarrow{CB}+\overrightarrow{AD}|= \\ =|\overrightarrow{KA}+\overrightarrow{AD}|=|\overrightarrow{KD}|= \frac{a \sqrt{2} }{2}$
$|\overrightarrow{CB}|-|\overrightarrow{CA}|+|\overrightarrow{CD}|=|\overrightarrow{CB}|-a+a=|\overrightarrow{CB}|= \frac{a \sqrt{2} }{2}$

nafanya2014_zn (413k баллов) 21 Март, 18