2.Найдите точку минимума функции у=(9-x)e9-x3.Найдите наименьшее значение функции...

$1) y=(9-x)*e^{9-x}$
$y'=((9-x)*e^{9-x})'=(9-x)(e^{9-x})'+e^{9-x}(9-x)'=$
$=e^{9-x}(9-x)'+(9-x)*e^{9-x}(9-x)'=e^{9-x}(9-x)'+(9'-x')*$
$*e^{9-x}(9-x)=e^{9-x}(9-x)'+e^{9-x}(9-x)(-x)'=$
$=e^{9-x}(9-x)'-e^{9-x}(9-x)x'=-9^{9-x}(x)'-e^{9-x}(9-x)(x)'=$
$=-e^{9-x}-1e^{9-x}(9-x)=e^{9-x}(x-10)$

Приравняем к нулю:
$e^{9-x}(x-10)=0$
$e^{9-x}=0$ $x-10=0$
Не подходит. $x=10$
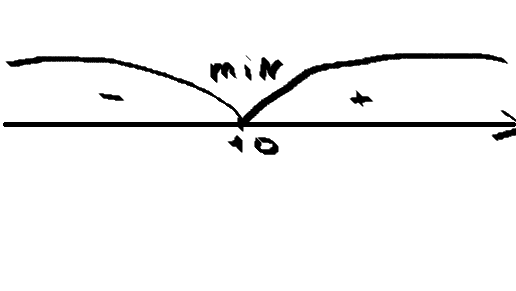
Рисунок смотри в вложении.
Ответ: 10

3) $\frac{cos2x-cosx+1}{2sinx- \sqrt{3} }=0$

$\frac{cosx}{ \sqrt{3} -2sinx}- \frac{2cos^2x}{ \sqrt{3} -2sinx} =0$

$- \frac{cosx(2cosx-1)}{ \sqrt{3} -2sinx}=0$

$\frac{cosx(2cosx-1)}{ \sqrt{3}-2sinx } =0$

cosx=0 при √3-2sinx≠0 | 2cosx-1=0 при √3-2sinx≠0
x=π/2 +πn; n∈Z и √3-2sinx≠0 | 2cosx=1 при √3-2sinx≠0
| cosx=1/2 при √3-2sinx≠0
| x=±arccos(1/2)+2πn; n∈Z и √3-2sinx≠0
| x=±π/3 +2πn; n∈Z и √3-2sinx≠0
Ответ: смотри выше (их 2)