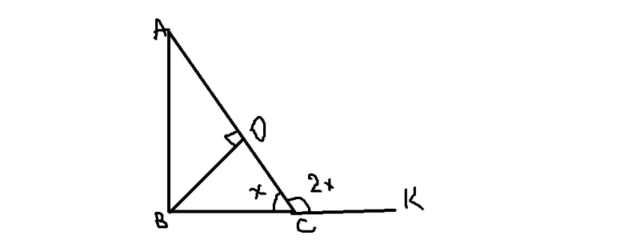
Смотри рисунок.
Пусть угол OCK=2х, тогда угол OCB равен х. Их сумма 180градусов, т.к. они смежные.
х+2х=180
3х=180
х=60 - это угол OCB.
Рассмотрим треугольник ОВС - он прямоугольный (угол ВОС=90градусов, угол ОСВ = 60 градусов) значит угол ОВС = 180-90-60=30 градусов
Запишем для угла OCB:
cos 60 = BC/AC поскольку по условию AC=100, имеем
cos 60= BC/100⇒ BC = 100× cos 60
cos 60 - это табличная величина = 1/2
BC= 100×1/2=50
Запишем для угла OBC:
sin 30 = OC/BC ⇒ OC= BC × sin 30= 50 × 1/2=25
sin 30 - это табличная величина = 1/ 2
Ответ: OC=25