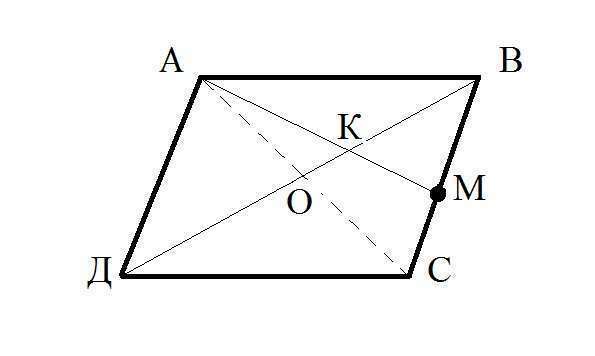
ВД является диагональю параллелограмма. Проведем еще одну диагональ АС. (см. рисунок во вложении). Диагонали пересекаются в точке О. В параллелограмме диагонали делятся пополам. Значит АО = ОС. По условию ВМ = СМ. Следовательно АМ и ВО являются медианами в треугольнике АВС. ВО = ДВ/2 = 12/2 = 6 см.. Т.к. ВО - медиана, то ВК:КО = 2:1. Следовательно, длина ВО в условных единицах = 2+1 = 3 Одна условная единица равна 6см/3 = 2 см. Значит ВК = 2ус.ед.* 2см = 4 см.
Ответ: ВК = 4 см.