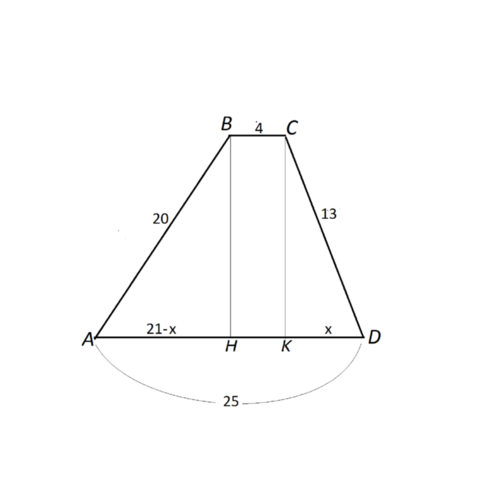
Обозначим вершины трапеции АВСD.
Опустим из вершин В и С высоты на АD
ВН=СК
Из прямоугольного треугольника АВН по т.Пифагора выразим высоту ВН
ВН²=АВ²-АН²
Из прямоугольного треугольника СКД выразим высоту СК
СК²=СD²-КD²
Пусть КD=х
Тогда АН=(25-4-х)=21-х
Из равенства ВН и СК составим уравнение:
АВ²-АН²=СD²-КD²
400-(21-х)²=169-х²
Получим 42х=210
х=5 см
Высоту найдем из треугольника СКD
СК=√(169-25)=12 см
Площадь трапеции равна половине произведения её высоты на сумму оснований.
S (ABCD)=12*29:2=174 см²