Добрый день)
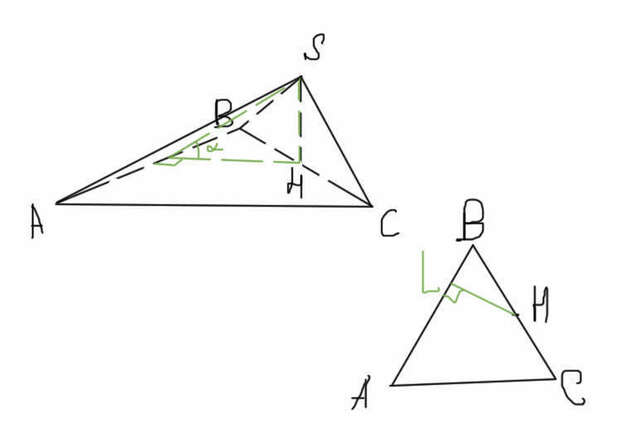
Объём пирамиды равен одной трети произведения площади основания на высоту, то есть (Sabc*SH)/3. Площадь равностороннего треугольника Sabc = a²(√3)/2, а значит, проблема только в том, чтобы найти SH. На чертеже я опустила из очки H перпендикуляр LH на сторону AB, LH = SH, так как треугольник LSH - прямоугольный с углом 45°, а LH и SH - его катеты.
Из треугольника BHL, в котором угол L = 90°, угол B = 60°, а BH = a/2 = 3 мы можем узнать LH = BH*sin60° = 3*(√3)/2.
Итак, V = (a²(√3)/2)*3*(√3)/2)/3 = (a²*3)/(3*4) = a²/4 = 36/4 = 9.
Надеюсь, помогла.