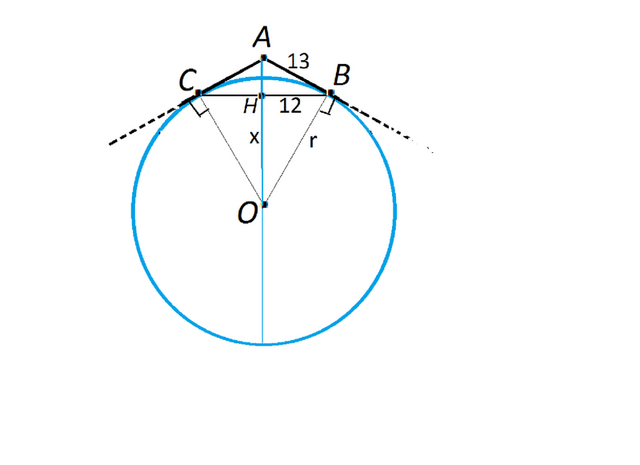
Сделаем и рассмотрим рисунок.
Пусть касательные проведены из точки А, а
С и В - точки касания.
По условию АВ=АС=13
ВС=24
АВС - равнобедренный треугольник.
Соединим А и центр О.
Треугольник ВОС равнобедренный.
АН - высота треугольника ВАС.
ОН - высота треугольника ВОС.
ВН=24:2=12
Из ⊿АНВ по т.Пифагора находим АН=5
OВ=r
Рассмотрим прямоугольный треугольник АВО.
ОН в нем - высота.
Высота прямоугольного треугольника, проведенная из вершины
прямого угла, есть среднее пропорциональное между отрезками,
на которые делится гипотенуза этой высотой
АН=5.
ВН²=5 ОН
144=5 ОН
ОН=28,8
Из прямоугольного треугольника ВНО:
ОВ²=ОН²+ВН²
OB=r
r²=28,8²+12²
r²=829,44+144=973,44
r=31,2
-----
[email protected]