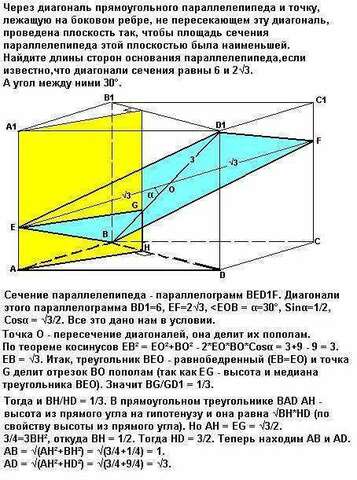
Строим сечение параллелепипеда, как указано в "дано".
Сечение параллелепипеда - параллелограмм BED1F. Диагонали его BD1=6, EF=2√3, Точка О - пересечение диагоналей, она делит их пополам.
По теореме косинусов EB² = EO²+BO² - 2*EO*BO*Cosα = 3+9 - 9 = 3.
EB = √3. Итак, треугольник ВЕО - равнобедренный (ЕВ=ЕО) и точка G делит отрезок ВО пополам (так как ЕG - высота и медиана треугольника ВЕО). Значит BG/GD1 = 1/3.
Тогда и ВН/НD = 1/3. В прямоугольном треугольнике ВАD АН - высота из прямого угла на гипотенузу и она равна √ВН*НD (по свойству высоты из прямого угла). Но АН = ЕG = √3/2.
3/4=3ВН², откуда ВН = 1/2. Тогда НD = 3/2. Теперь находим АВ и АD.
АВ = √(АН²+ВН²) = √(3/4+1/4) = 1.
АD = √(АН²+НD²) = √(3/4+9/4) = √3.
Ответ: стороны основания параллелепипеда равны 1 и √3.
P.S. Если успею, рисунок переделаю. НЕ очень понятный получился...