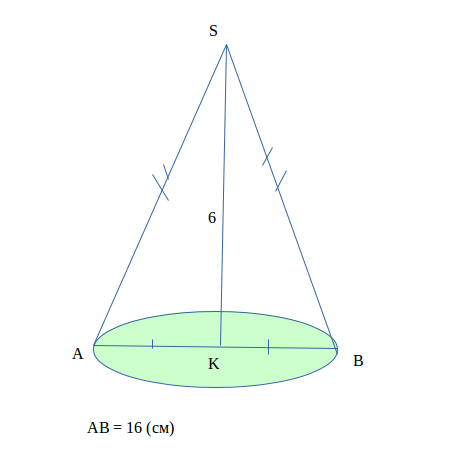
Дано:
ASB - конус, AS = SB - образующая, SK = 8 (см), AB = 16 ( см ), AK = BK - радиус основания.
Найти: S(бок).
Решение:
Радиус основания в два раза меньше диаметра AB
AK = AB/2 = 16/2 = 8 (см).
С прямоугольного треугольника SKA
AS² = AK²+SK²
AS = √(AK²+SK²) = √(8²+6²)=√100 = 10 (см).
Теперь площадь боковой повехности
S(бок) = π*r*l=π*8*10 = 80π (см²).
Ответ: 80π (см²).