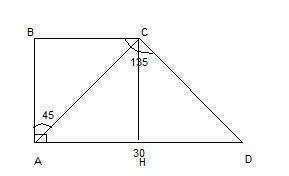
Рассмотрим треуг-ик АВС. Угол В - также прямой в прямоугольной трапеции. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, найдем угол АСВ:
Значит, прямоугольный треуг-ик АВС - равнобедренный, т.к. углы при его основании АС равны.
АВ=ВС
Рассмотрим треуг-ик ACD:
Таким образом, прямоугольный треуг-ик ACD - равнобедренный с равными углами при основании AD. Построим высоту трапеции СН, которая будет равна короткой стороне АВ и разделит ACD на два равных прямоугольных треугольника АНС и DHC. В равнобедренном треуг-ке высота, проведенная к основанию, является также и медианой, значит
АН=DH=30:2=15 см
В прямоугольных равных треугольниках АНС и DHC углы АСН и DCH равны также по 45 градусов (90-45=45°). Это тоже равнобедренные треугольники, где
АН=DH=CH=15 см. Значит, и АВ=15 см
Имеется три равных прямоугольных равнобедренных треугольника АВС, АНС и DHC с равными катетами по 15 см.