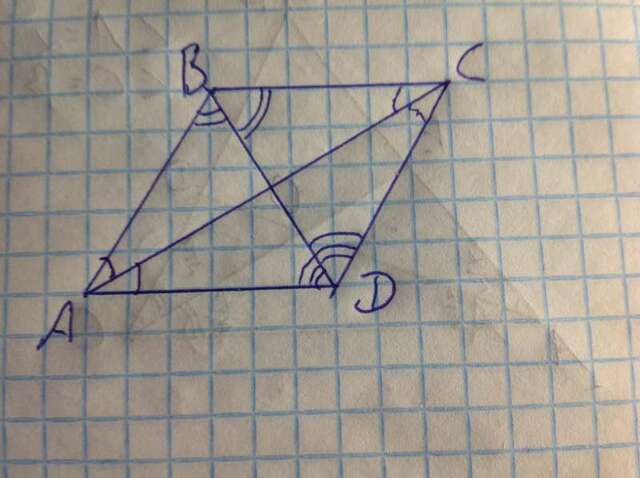
Пусть в четырехугольнике ABCD диагональ AC является биссектрисой углов А и С, а диагональ ВD является биссектрисой углов В и D (см. рисунок).
Докажем, что противоположные углы четырехугольника равны. Рассмотрим треугольники АВD и ВСD. Угол ВАD треугольника АВD равен 180-АВD-ВDА. Угол С треугольника ВСD равен 180-DВС-СDВ. Так как АВD=DВС, а ВDА=СDВ, получаем, что углы А и С четырехугольника равны. Аналогично, рассмотрим треугольники АВС и АDС. В треугольнике АВС угол В равен 180-ВАС-ВСА, в треугольнике АDС угол D равен 180-DАС-DСА Углы ВАС и DАС, ВСА и DСА попарно равны, тогда углы B и D также равны.
Теперь рассмотрим треугольник АВС. Так как углы А и С равны, равны и углы САВ и ВСА. Тогда треугольник равнобедренный и АВ=ВС. Аналогично, рассмотрим треугольник ВСD, в нём углы СВD и СDВ равны, тогда он также равнобедренный и СD=ВС=АВ. Наконец, треугольник АСD также равнобедренный с основанием АС, поэтому АD=СD=ВС=АВ. То есть, все стороны исходного четырехугольника равны, тогда он является ромбом.