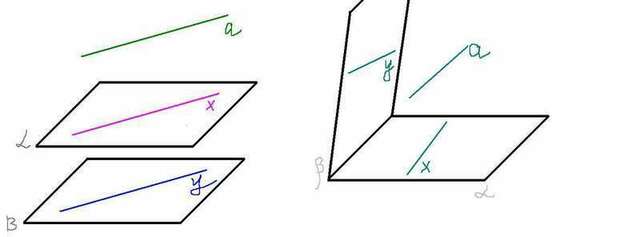
1) Выберем на плоскости α некоторую прямую с, параллельную прямой а. Так как а||b по условию и a||c, то получим, что b||c. По признаку параллельности прямой и плоскости (если прямая параллельна какой-либо прямой, лежащей в плоскости, то она параллельна и всей этой плоскости) получаем, что прямая b параллельная некоторой прямой лежащей в плоскости α, значит b||α.
Ответ: да, следует
2) Однозначного ответа нет, так как может выполниться признак параллельности плоскостей (если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны) и при этом эти две плоскости будут параллельные прямой а.