задание 1. Три прямые, проходящие через точку М, пересекают четвертую прямую в точках...

Question

задание 1. Три прямые, проходящие через точку М, пересекают четвертую прямую в точках А,В,С соответственно. Докажите, что все четыре точки лежат в одной плоскости.
задание 2. Дан куб ABCDA1B1C1D1 MэAA1, HэDD1, MA=/=HD. Построить: а) точку пересечения прямой MH с плоскостью (ABC); б) точку пересечения прямой MH с прямой A1D1; в) Линию пересечения плоскостей (MHC) и (ABC).

Answer 1

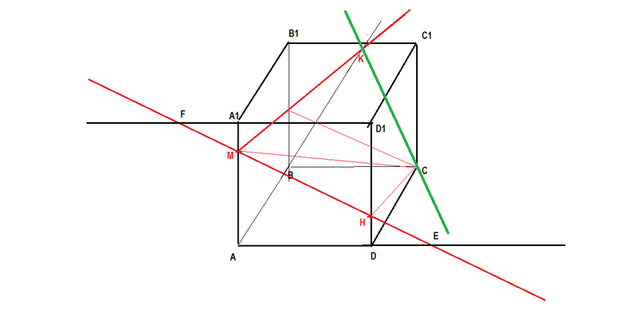
задание 2

сделаем построение по условию

M принадлежит AA1,

H принадлежит DD1,

MA не равно HD.

Построить:

а) точку пересечения прямой MH с плоскостью (ABC);

прямые (МН) и (AD) лежат в одной плоскости (AA1D1D)

продолжим их до пересечения в точке Е

НО прямая (AD) лежит в плоскости (АВС) -

- значит точка Е будет также точкой пересечения прямой MH с плоскостью (ABC);

б) точку пересечения прямой MH с прямой A1D1;

прямые (МН) и (A1D1) лежат в одной плоскости (AA1D1D)

продолжим их до пересечения в точке F

в) Линию пересечения плоскостей (MHC) и (ABC).

для построения линии пересечения достаточно найти ДВЕ общие точки

соединим точки М,Н,С - получим плоскость (МНС)

точка С - первая общая точка

на грани (АА1В1В) через т М проведем прямую (МК) параллельную  (НС) до

пересечения с прямой (АВ)  в точке К

прямые (МК) и (НС) параллельны, значит (МК) лежит в плоскости (МНС)

прямая (АВ) лежит в плоскости (АВС)

точка К - вторая общая точка

проведем прямую (СК) через две точки - это линия пересечения плоскостей

 

---