Точка М лежит вне плоскости треугольника АВС. Точки Р,К,Е,Н середины отрезков...

Question

Точка М лежит вне плоскости треугольника АВС. Точки Р,К,Е,Н середины отрезков АВ,МА,МС,ВС. Доказать что четырехугольник РКЕН-параллелограмм

Answer 1

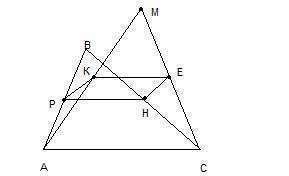
Рассмотрим треугольник АВС. Точки Р и Н - середины двух его сторон, значит, РН - средняя линия треугольника. Следовательно,
PH II АС, PH=1/2 АС.
Рассмотрим треугольник АМС. Здесь точки К и Е - середины двух его сторон, значит, КЕ - средняя линия треугольника, и
KE II AC, KE = 1/2 AC.
Т.е. мы имеем, что  PH II АС и KE II AC, значит, PH II КЕ.
Также PH=1/2 АС и KE = 1/2 AC, значит РН=КЕ.
Пользуемся одним из признаков параллелограмма: если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм. РКЕН - параллелограмм.

---