Здесь в условии ошибка. Должна быть не окружность, а прямая через D.
Это отрезок DK, длину которого нам надо найти.
Точка К должна находиться на отрезке АВ, потому что отрезок DB явно делит трапецию на такие части, что S(BCD) < S(ABD).
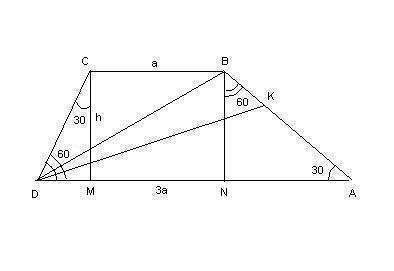
Вот рисунок. Из него ясно, что:
AB = BN/sin 30 = 2*BN = 2h, AN = BN*tg 60 = h√3
DM = CM*tg 30 = h√3/3, CD = DM/sin 30 = 2*DM = 2h√3/3
AD = DM + MN + AN = h√3/3 + a + h√3 = 3a
4h√3/3 = 2a
h = 3a/(2√3) = a√3/2
AB = 2h = a√3
CD = 2h√3/3 = 2a√3/2*√3/3 = a
Угол BCD = 180 - ADC = 180 - 60 = 120
Треугольник BCD - равнобедренный с боковой стороной а и углом 120.
Угол CBD = 30
Из теоремы косинусов
BD^2 = CD^2+BC^2-2*CD*BC*cos 120 = a^2+a^2-2a^2*(-1/2) = 2a^2+a^2 = 3a^2
BD = a√3 = AB.
S(BCD) = 1/2*BC*CD*sin BCD = 1/2*a^2*√3/2 = a^2*√3/4
Угол ABC = 180 - 30 = 150, ABD = ABC - CBD = 150 - 30 = 120.
Треугольник ABD - равнобедренный с боковой стороной а√3 и углом 120.
S(ABD) = 1/2*AB*BD*sin ABD = 1/2*a√3*a√3*√3/2 = 3a^2*√3/4 = 3*S(BCD)
Площадь всей трапеции
S(ABCD) = (3a + a)*h/2 = 4a*(a√3/2)/2 = a^2*√3
Значит, S(AKD) = S(KBCD) = a^2*√3/2 = 2*S(BCD)
То есть S(BKD) = S(BCD)
S(BKD) = 1/2*KB*BD*sin KBD = 1/2*KB*a√3*sin 120 = a^2*√3/4
KB*a√3/2*√3/2 = a^2*√3/4
KB = a/√3 = a√3/3
Из теоремы косинусов
DK^2 = BD^2 + KB^2 - 2*BD*KB*cos 120 = 3a^2 + a^2/3 - 2*a√3*(a√3/3)(-1/2) =
= 3a^2 + a^2/3 + a^2 = 13a^2/3
DK = a*√(13/3) = √39*√(13/3) = √(13*3*13/3) = 13